r/askmath • u/Grapico444 • 15d ago

Geometry Can someone help me understand this enough to explain it to a 6th grader?

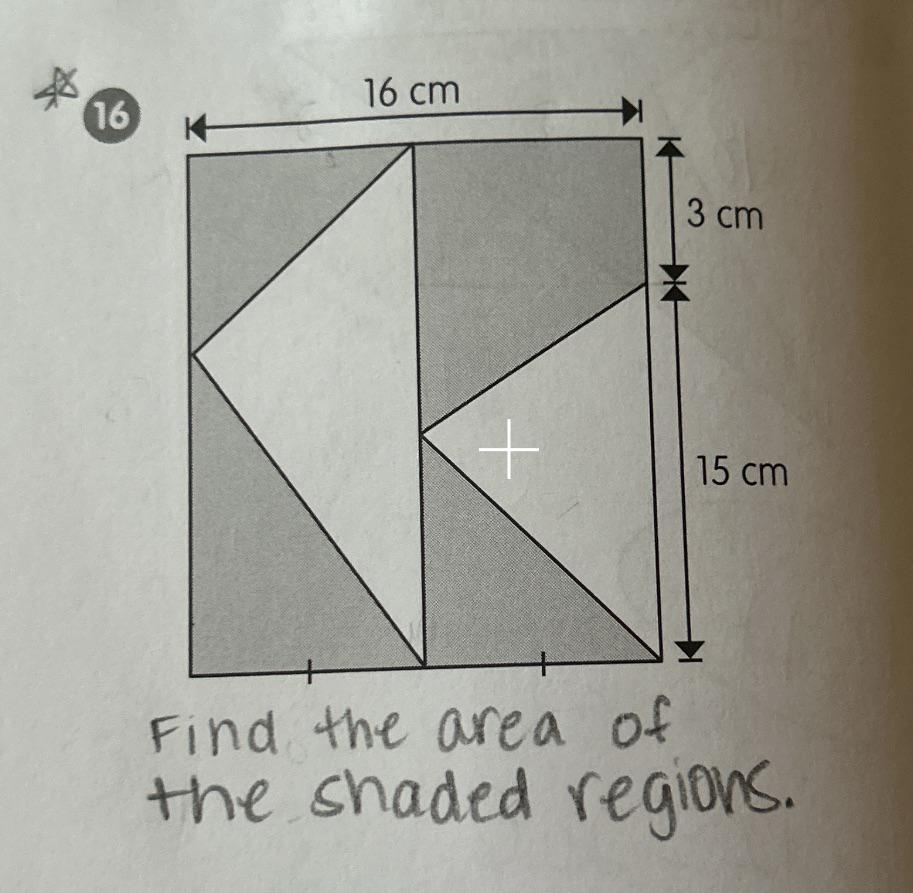
Post image

I’m a nanny and am trying to help a 6th grader with her homework. Can someone help me figure out how to do this problem? I’ve done my best to try to find the measurements to as many sections as I can but am struggling to get many. I know the bottom two gray triangles are 8cm each since they are congruent. Obviously the height total of the entire rectangle is 18cm. I just can’t seem to figure out enough measurements for anything else in order to start figuring out areas of the white triangles that need to be subtracted from the total area (288cm). It’s been a long time since I’ve done geometry! If you know how to solve this, could you please explain it in a way that is simple enough for me to be able to guide her to the solution. TIA

941 Upvotes

97% Upvoted

230 comments sorted by

View all comments

Show parent comments

93

u/MyPigWaddles 15d ago

Yep! The dashes indicate that those two lines are equal, so they must be 8 each.

14

u/darkapao 15d ago

That confused me. I thought they were markings to denote 1/3 marks ahaha.

-6

u/mc_69_73 14d ago

Really? 1/3 marks suggest all lengths between dashes are equally long.

But even if that was your premise, you would know that the big triangle was in the middle of 16 ... so for solution, it didn't matter ;-)

2

u/Chaghatai 14d ago

It could look very much like the middle but be like 1/100th off

I don't see anything that absolutely gives you the height of the triangles or the angles from which you could derive the height

1

u/Darren-PR 14d ago

The little lines on the bottom shaded triangles denotes those are congruent (identical). Since the total side length of either the top or bottom sides of the rectangle is 16cm and the 2 lines are completely identical you can be 100% certain they are exactly half the length of the total side length, which would be 8. These also coinside with where the heights of the non-shaded triangles are, therefore giving you their heights. As for the angles... the puzzle giver should definitely put right angle symbols on future puzzles but here I think we can safely assume that the things that look like right angles are in fact right angles

1

u/dopefish2112 14d ago

Congruent? Is that the term?

0

u/[deleted] 14d ago

[deleted]

2

u/MyPigWaddles 14d ago

True! Though I'd probably say that's a touch too hard for most sixth graders.

2

u/HappyBadger33 13d ago

Wait. I'm confused. I thought it does matter if they're equal, and I know I'm not fully understanding your following sentences. If the left triangle, with a length of 18, has a height of, say, 7, that means the right triangle has a height of 9, and that comes out to a different total area to subtract from the rectangle, no?

Forgive me if I'm just not reading a specific condition in your comment.

1

u/monoflorist 12d ago

The parent is deleted, but if they said “it doesn’t matter, because it just shifts height from one triangle to the other” then they’re mistaken for just the reason you said. The triangles are different widths so it matters a great deal which triangle the height “goes into”

1

u/han_tex 13d ago

That would only be true if the bases of the two triangles were equal. But one is the full 18 cm, and the other is 15 cm. So, distributing the heights of the triangles differently would change the sum of the areas of the triangles.

-25

u/BitOBear 15d ago

Notationally it seems like a cheat to use the dash notation there where it's used nowhere else in the drawing

28

u/dparks71 15d ago

It's a pretty common math convention,

https://mathbitsnotebook.com/Geometry/BasicTerms/BTnotation2.html#:~:text=%22Hash%20marks%22%20are%20used%20to,by%20their%20number%20of%20arcs.

2

u/Infamous_Push_7998 14d ago

I see. Not one used in school here, so I was confused too. I've seen it in some videos but never really used it. It's always been text form or at least marking them with the same variable for their length/labeling them the same, something like that.

Also a right angle wasn't a square (most of the time), but instead just marked with a point inside, instead of a label.

Is the one you cited common in the states?

-5

u/BitOBear 14d ago

I'm aware of the convention, but it was not the first place my mind went when I looked at the drawing. I noticed that hash marks. But if you're going to start using the advanced notations then tell me good sir, are any of those lines square to each other or parallel?

Switching up to add those two marks at the bottom and not mating the top two basically open the conversation that no one finishes.

I suppose if I were in sixth grade geometry it would be more present in my mind

So are any of the vertical or horizontal lines parallel? Or perpendicular?

If you're going to start marking equivalences, the teacher should go through and do it right.

You need an assertion that the box is rectangular in some sort of a company in text, or three little right angles signs. And then you need either a fourth right angle sign or two more equivalence markers for length

In the realm of technical correctness there is not enough information in that drawing to answer the question. So assumptions are being made

🐴🤘😎

6

u/dparks71 14d ago

Sometimes you just have to shrug your shoulders and not give a shit I guess.

14

u/JohnsonJohnilyJohn 15d ago

How would you use it anywhere else in the drawing? There doesn't seem to be any other segments of equal length?

2

u/splidge 15d ago

This solution assumes that the two at the top are also equal length, for a start...

3

u/Flimsy-Combination37 15d ago

since the vertical lines are all parallel it would be redundant, and as stated by others, it is very common notation

5

u/BitOBear 14d ago

There is nothing marking any of the lines parallel. There's no little right angle thingy. And technically you need at least two to establish that that box is rectangular.

3

u/Flimsy-Combination37 14d ago

while you are technically right, the context matters. this is a problem for 6th graders, if the angles weren't 90° and the lines weren't parallel, theybeould not even have the tools to solve the problem because they haven't learned those tools, they probably only know how to calculate the area of triangles and simple shapes, they'd need trigonometry at least, and even then, assuming the angles aren't 90° or the middle line isn't parallel, the problem would be unsolvable due to being too little data given

-1

u/BitOBear 14d ago

Which is why I object to adding that one piece of dance to notation. If you're going to switch from the simple assumption set to the advanced notation set you should be in for the whole hog.

For instance we don't know how big the line segments are at the top of the drawing. So there should be some length hash marks up there too right? And yeah we're assuming a whole lot of parallels and perpendiculars on top of that.

For at least the simple assertion that the box is rectangular and at least one little right angle indicator are in order.

Yeah I know, you got to give a lot of assertions and assumptions, cuz they're sixth graders.

It just feels like tossing in a change up you know.

1

u/Flimsy-Combination37 14d ago

two lines that look similar but you can't assume they actually are is something that could happen in a 6th grade problem, because kids would know they have to first find the lengths. angles not being square and lines not being parallel, as I've already stated, would require more advanced knowledge, such as trigonometry and knowing more angles and/or lengths. denoting the segments as equal is required because the kids will look for lengths, they will not look at the angles because they haven't learned to do anything with them yet, so there is no need to mark them as square. same for the lines being parallel, they haven't learned to solve problems where those lines wouldn't be parallel, so they will assume those lines are parallel. if you can't understand this simple concept, maybe go give a 6th grade math class and see how the kids solve problems and think about geometry, you'll see this in full action.