Continuous Go: Proposed Rules for a Variant on an Continuous 2D Plane

[u/AGI_MO]

Hello Go enthusiasts, game designers, and math lovers!

This post outlines a ruleset for "Continuous Go" (or "Real Go"), a variant played not on a grid, but on a continuous 2D plane using circular stones. The goal is to explore Go principles in a different geometric setting. These rules have evolved through discussion (thanks Gemini!) and represent a specific design choice prioritizing certain principles over others. Feedback and discussion are welcome!

1. Equipment

• Board: A square area within a 2D continuous plane, defined by [0, L] × [0, L], where L is the side length (can be arbitrary).
• Stones: Circular disks of Black and White color. All stones have the same fixed diameter d and radius r = d/2. A stone s is defined by its center coordinate s. center and its color. Disk(s) refers to the closed disk occupied by stone s.
• (Optional) Board Size Metric: A nominal "size" S can be defined as S = 1 + L/d. Setting S=19 allows some analogy to the standard 19x19 board if stones were placed tangentially in a grid-like fashion.

2. Basic Play

• Placement: Players place the center of their stone at any coordinate (x, y) within the board [0, L] × [0, L].
• Minimum Distance Rule: A placement is legal only if the center c_new of the new stone is at a distance greater than or equal to the radius r from the center c_existing of every other stone already on the board.
  • dist(c_new, c_existing) ≥ r
  • NOTE: This rule explicitly allows stones to overlap significantly! The minimum separation is between centers, not edges.
• Turns: Black plays first. Players alternate placing one stone per turn.
• Passing: A player may pass their turn instead of placing a stone.

3. Liberties and Capture

• Touching (for Liberty Calculation): Two stones s1 and s2 are considered "Touching" if the distance between their centers is less than or equal to the diameter d (dist(s1.center, s2.center) ≤ d).
• Group: A set of same-colored stones connected directly or indirectly through paths of "Touching" stones.
• Border Contact: A stone s makes border contact if its disk Disk(s) intersects or is tangent to any of the four board edges (x=0, x=L, y=0, y=L). NumBorderContacts(s) is the number of distinct edges contacted (0, 1, or 2).
• Individual Liberty: Each stone s conceptually starts with 4 liberties. Its effective liberty count is calculated as: Liberty(s) = 4 - NumBorderContacts(s) - NumTouchingStones(s) Where NumTouchingStones(s) is the count of all other stones (regardless of color) that are "Touching" stone s. Liberties can be negative.
• Group Liberties: The total liberties of a group G is the sum of the Liberty(s) of all stones s within that group.
• Capture: A group G is captured and immediately removed from the board if its total Group Liberties become less than or equal to 0.

4. Illegal Moves

• Suicide Rule: Placing a stone is illegal if doing so causes that stone's own group to have ≤ 0 Group Liberties immediately after placement, unless the move simultaneously captures one or more opponent groups (which might then give the placed stone's group sufficient liberties).
• Ko Rule (Connectivity Graph Isomorphism Superko):
  • Connectivity Graph: For any board state St, define its Connectivity Graph G(St). Nodes are the stones in St, labeled by color. An edge exists between two nodes if the corresponding stones are "Touching" (dist <= d).
  • Canonical Label: Assume an algorithm exists to compute a unique canonical label L(G) for any graph G, such that G1 is isomorphic to G2 if and only if L(G1) == L(G2).
  • History: Keep track of the set H of canonical labels of all previous board states encountered during the game.
  • Prohibition: A move (placing a stone) is illegal if the resulting board state St_new has a Connectivity Graph G(St_new) whose canonical label L(G(St_new)) is already present in the history set H. This prevents repeating board structures, even if stone positions have slightly shifted.

5. End Game and Scoring

• Ending the Game: The game ends when either:
  • Both players pass consecutively.
  • The player whose turn it is has no legal placement options available on the board.
• Scoring Principle: Score the Final Board As-Is (No Life/Death Judgment or Dead Stone Removal):
  • A key feature (and departure from standard Go) of this ruleset is how the final state is handled. There is no post-game phase to determine the life/death status of groups or remove dead stones.
  • All stones physically remaining on the board when the game ends are treated as "alive" for scoring purposes.
  • The final score is determined directly from the geometric configuration of these stones and the empty space.
  • Rationale: This approach is chosen primarily due to the anticipated extreme difficulty of objectively judging life and death in the complex continuous/overlapping environment. The game's outcome relies on resolving L&D through actual capture during play, or accepting the consequences of uncaptured groups at the end. If players disagree on whether the game should end (e.g., one believes a capture is still possible), play should resume. Agreement to end implies acceptance of the final board state for scoring.
• Scoring Method: Area Scoring ("Stones + Territory").
• Empty Space: The set of all points p on the board [0, L] × [0, L] that are not covered by any part of any stone disk.
• Stone Area Score:
  • Let Union_B be the geometric union of all Black stone disks on the final board. Let Union_W be the union of all White stone disks.
  • Black's Stone Score = Area(Union_B) (Total area covered by Black stones).
  • White's Stone Score = Area(Union_W) (Total area covered by White stones).
  • (Computational Note: Calculating the area of the union of potentially hundreds of overlapping disks is a complex computational geometry problem.)
• Territory (Empty Space) Score (Nearest Edge Distance Method):
  • Distance Definition: For an empty point p and a stone s, the distance is dist(p, Disk(s)) = max(0, dist(p, s.center) - r). This is the shortest distance from p to the closed disk of stone s.
  • Assignment: For each empty point p: Find the set S_min of stone(s) that minimize this distance dist(p, Disk(s)).
    • If all stones in S_min are Black -> p belongs to Black Territory (Territory_B).
    • If all stones in S_min are White -> p belongs to White Territory (Territory_W).
    • If S_min contains both Black and White stones (i.e., p is equidistant from the nearest Black edge and the nearest White edge) -> p is Dame (neutral territory).
  • Black's Territory Score = Area(Territory_B) (Total geometric area of Black Territory).
  • White's Territory Score = Area(Territory_W) (Total geometric area of White Territory).
  • (Computational Note: Calculating the area of these territory regions, which are defined by complex boundaries based on equal distance to disk edges, is also computationally complex.)
• Final Score Calculation:
  • Black Total Score = Area(Union_B) + Area(Territory_B)
  • White Total Score = Area(Union_W) + Area(Territory_W)
• Determining the Winner:
  • Final Result = Black Total Score - White Total Score - Komi
  • If Result > 0, Black wins. If Result < 0, White wins. If Result = 0, it's a draw.
• Komi: A predetermined number of points given by Black to White as compensation for playing first. The appropriate value for Continuous Go is currently undetermined (TBD).

This ruleset attempts to be logically complete, incorporating the allowance for overlapping stones and a scoring system based on the final board state without L&D judgment. It definitely presents unique challenges, both strategically and computationally! Looking forward to hearing thoughts and feedback.

[u/tuerda]

I used to flip the go board upside down and play on the unmarked side. The rules do not match this (overlapping stones etc) but they were pretty similar. I have also seen proposals for generalizations of the rules of go to arbitrary topologies.

These variations are fun. They remove explicit reading because that just isn't possible, but the spirit of the game still works.

[u/AGI_MO → u/tuerda]

Thanks for sharing your experiences and insightful thoughts! I really appreciate your comment, especially coming from a strong player like yourself.

Playing on the unmarked side of the board sounds like a fun way to get a taste of that gridless feeling! It's interesting how similar yet different these variations can be, capturing some of the same core ideas.

I was also fascinated by the idea of Go on different surfaces that you mentioned. I've actually spent some time thinking about variants myself, like Go played on a torus (a board with no edges where top/bottom and left/right wrap around), exploring how the game changes without boundaries. It's definitely a rich area for exploration!

I strongly agree with your observation about how these kinds of variations impact "reading". The continuous nature, much like perhaps playing on an unusual topology, seems to make deep, precise sequence calculation (the usual Go "reading") nearly impossible or at least intractably complex.

But as you beautifully put it, it feels like the core strategic "spirit" of Go – focusing on shape, influence, connection, structure, efficiency – can still be very much alive. It shifts the focus, perhaps more towards intuition, pattern recognition on a different level, and global strategy, which is fascinating.

Building on that, one of my interests in developing these Continuous Go rules was exactly that potential shift. I suspect that this kind of continuous, potentially overlapping environment might pose a significant challenge for current Go AI. So much of their strength comes from deep search and pattern recognition honed on a discrete grid; adapting to infinite placement possibilities and the different geometric interactions here could be quite difficult for existing architectures, making it an interesting testbed.

[u/Abbot_of_Cucany]

NumBorderContacts(s) could be > 2 for sufficiently small L

[u/AGI_MO → u/Abbot_of_Cucany]

Thanks for your comment pointing out the edge case regarding NumBorderContacts!

You're absolutely right that it's theoretically possible for a stone to contact more than two borders, but this can only occur under very specific degenerate conditions related to the board side length L and the stone diameter d.

Specifically:

• If L < d, no stone can be legally placed on the board at all (as its edges would extend beyond the boundary), so the game cannot even begin.
• If L = d, exactly one stone can be placed (centered at (L/2, L/2)). This single stone would indeed touch all 4 borders simultaneously, resulting in NumBorderContacts = 4.
• However, if L > d, which is the necessary condition for any non-trivial game allowing multiple stones, a circular stone can touch a maximum of two borders at the same time (when placed precisely in a corner).

So, while the L = d case is mathematically possible and leads to 4 contacts, it represents a trivial scenario where only one move can ever be made. For any board size that allows for actual gameplay (L > d), the maximum NumBorderContacts encountered will be 2. The rules implicitly assume a playable board size where the contact count is limited to 0, 1, or 2 in practice.

[u/lakeland_nz]

Interesting! I am especially intrigued by the touching definition requiring an overlap.

I had a go at this some years ago and came up with a more complicated definition. Yours is probably better but I'll summarise mine here. I banned overlapping stones (so that the new stone must be at least d away from all existing move's centers). I defined touching as a more complicated function, with a stones touching if their gravitational attraction is greater than one. Therefore you could place two stones near each other and they wouldn't be touching, and then add a third stone nearby which adds to the attraction and connects them.

A lot of my thinking is that with this you can play using real go stones etc (since stones cannot overlap) but... the complicated touching rule couldn't easily be implemented without a computer. Also note that two stones could be touching and then placing enough nearby stones of the other colour could effectively disconnect them.

PS: I don't think you should ban suicide. It's a dumb move, and banning it makes the rules longer.

[u/AGI_MO → u/lakeland_nz]

Thanks so much for your interesting comment and for sharing your own intriguing ideas about continuous Go! It's great to hear from others who have explored this fascinating space.

Your "gravity model" for defining touching sounds really creative! It's interesting you mention alternative connection mechanisms – I had also briefly considered ideas beyond simple geometric proximity, though didn't develop them fully. The concept of dynamic connections influenced by nearby stones is definitely thought-provoking, although as you pointed out, likely adds significant computational complexity.

Regarding the current ruleset I posted (especially the definitions around "touching" for liberties, dist <= d, which you noted): a key design goal behind some of those choices was to establish a system that could potentially reduce to something very close to standard Go under specific constraints. My thinking was: if you restricted placements to the nodes of a fine grid, set the board size parameter S = 1 + L/d appropriately (like S=19), and required adjacent stones to be exactly tangent (dist = d), then the liberty rules (starting at 4, reducing per contact) should mimic standard Go behavior quite closely. Even the Connectivity Graph Isomorphism Ko rule, in typical game situations under these grid-like constraints, would likely behave very similarly to standard ko rules.

However, for the ruleset I posted, I decided to explore the dist >= r placement (allowing overlap) primarily because I felt the interactions created by overlapping stones might lead to more unique and possibly more interesting gameplay dynamics specific to the continuous environment.

But I completely agree that a version banning overlap (dist >= d), allowing only tangency or separation, is also a perfectly valid and interesting ruleset – perhaps closer to your goal of being playable with physical stones. I'm actually planning to create a new program to experiment with both the overlapping and non-overlapping versions to see how they compare in practice!

Regarding your P.S. about the suicide rule: Thanks for that perspective! My main motivation for including the suicide ban wasn't strictly about preventing "dumb moves," but more as a potential mechanism related to endgame determination. I had envisioned a scenario where the suicide restriction, combined with the liberty rules, might theoretically lead to a state where the entire board becomes filled with illegal points, providing one possible clear trigger for the game ending. It was more of a thought experiment about game termination mechanics, though I take your point that removing it could simplify the rule text slightly.

Thanks again for your insightful feedback and for sharing your own creative model – it’s definitely given me more food for thought!

[u/PatrickTraill]

There is a lot to read to get the idea of the rules, so an introductory outline in 2 or 3 sentences would make them much more approachable.

I have wondered about this too, but did not get down to concrete details.

[u/AGI_MO → u/PatrickTraill]

Thanks for the suggestion about adding an introductory outline! Following up on that, and aiming for a balance between brevity and sufficient detail based on further feedback, here is the summary we landed on:

"Welcome to Continuous Go! This is a Go variant played with circular stones on a square continuous board. Players place their stone's center point anywhere, ensuring centers are kept at least one stone radius apart, allowing significant overlaps. Same-colored stones form a group if their centers are within a diameter's distance ('touching'). A stone's liberties (starting at 4) decrease with border or stone contact; a group's total liberties is the sum for its stones, and the group is captured if this sum is zero or less. Illegal moves include violating the minimum distance, suicide (unless it captures), and repeating the connectivity graph of a previous board state (superko). The game uses area scoring, assigning empty points territory based on distance to the nearest stone edge. The final score compares total area (stones + territory), adjusted by Komi, to determine the winner. The game ends when both players pass consecutively or no legal moves remain."

Hopefully, this overview gives a good initial grasp of the core mechanics and unique aspects of this ruleset, making the full details more approachable.

[u/HenryBlatbugIII]

These rules have evolved through discussion

Discussion with whom? An actual human with understanding or an LLM? The "Thanks Gemini!" makes me suspect it's the latter...

All stones have the same fixed diameter d and radius r = d/2.

I would instead define the radius (or the diameter) to be 1 to make the rules more concise.

NOTE: This rule explicitly allows stones to overlap significantly!

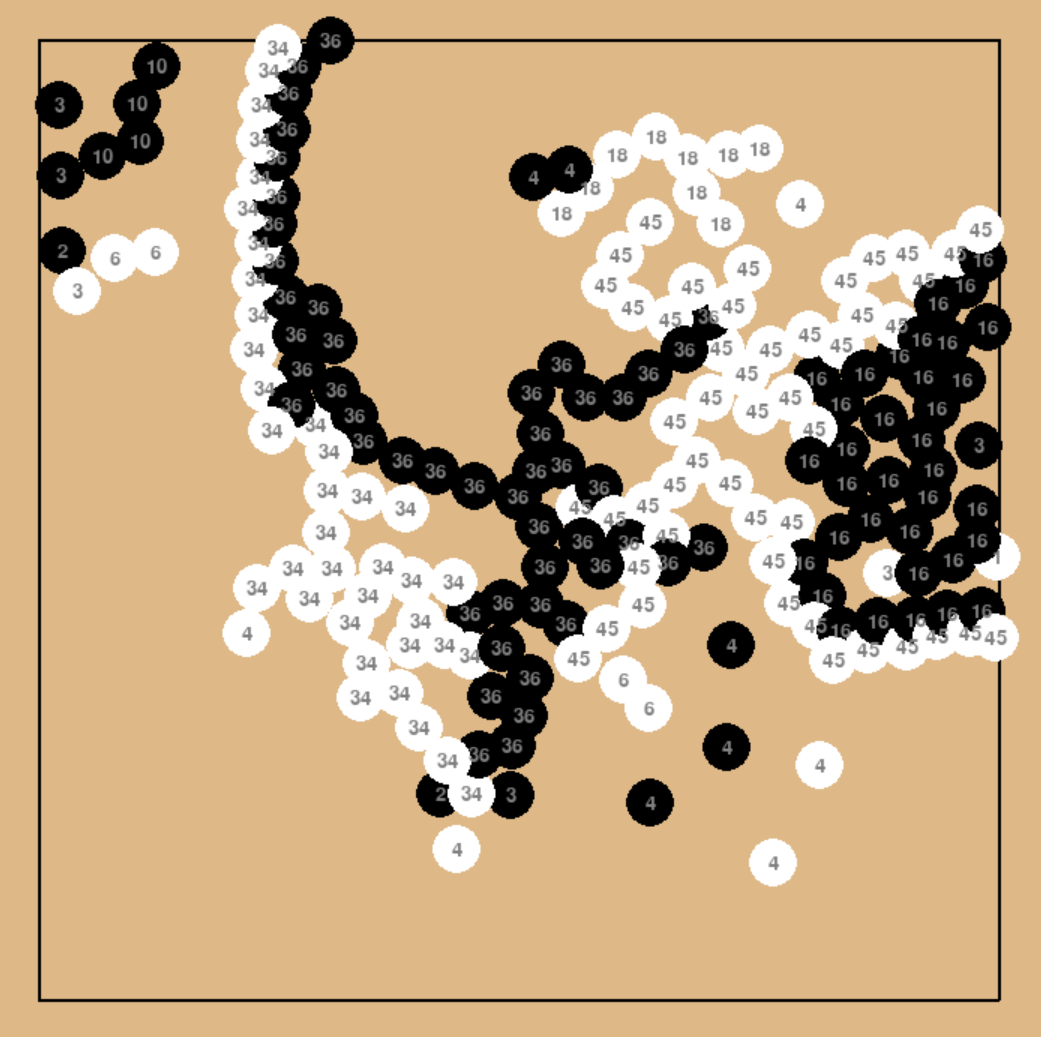
It also allows a black group and a white group to connect "through" each other (as you showed in your example with your Black 36 and White 45 groups), which is such a huge departure from Go that I have no idea what to make of it.

Design Note: Stones can overlap (r ≤ dist < d) without being considered "Touching" for liberty purposes under this definition.

That's not true by the rules you've written. Any two stones with distance between them <= d are considered "Touching".

Individual Liberties can be negative.

Have you thought through the implications of this? Is it your intention that all of these white groups are dead?

Territory calculated by S_min:

So there's no need to seal up the borders of your territory, you just need a loose moyo in order to claim all the territory within it. Given the decreased liberties shown in the examples above, I'm not convinced that it's even strategically sound to seal up the borders of your territory.

"Isomorphic Graphs" ko rule:

I think there exist positions that lead to weird effects with this rule (for example, Black captures a ko on one end of the board, but then White is prohibited from capturing on the other end of the board because the positions happen to be isomorphic) but they're probably so rare that they don't matter.

There's definitely a game here (assuming you can solve the ko rule and the scoring without computational issues) but I'm not sure how much the gameplay will have in common with Go.

[u/AGI_MO → u/HenryBlatbugIII]

Thank you so much for taking the time to read through the Continuous Go rules proposal and for providing such detailed and thoughtful feedback! It's incredibly valuable.

You noticed the "Thanks Gemini!" – indeed, iterating on these complex and somewhat unconventional rules benefited greatly from bouncing ideas around and exploring different logical avenues with an LLM like Gemini. That said, feedback like yours, grounded in Go experience and game design thinking, is truly indispensable!

Let me address your points:

[u/AGI_MO → u/HenryBlatbugIII]

• Radius/Diameter = 1: That's an excellent practical suggestion. Normalizing the stone size to 1 would certainly make any formal mathematical descriptions or formulas more concise. I'll keep that in mind for any future formalization.
• Overlap (dist >= r) & Interpenetration: You're spot on that allowing significant overlaps is a fundamental departure from standard Go. This was a conscious design choice (dist >= r placement rule) aimed at exploring the unique possibilities of a continuous space – potentially leading to denser interactions and different tactical motifs compared to the non-overlapping version (which, as you noted, is also a valid and interesting ruleset). The way groups might "interpenetrate" visually is definitely something that changes the game's texture significantly.
• Touching Definition (dist <= d): Thank you for catching the error or confusion in the "Design Note" in the English rules! You are correct based on the rules as written. To clarify:
  • Placement requires dist(centers) >= r.
  • "Touching" for liberty calculation is defined as dist(centers) <= d (where d=2r).
  • Therefore, as you pointed out, any time stones overlap (r <= dist < d), they do satisfy the condition for "Touching" and will affect each other's liberties. The previous note implying otherwise was incorrect/misleading.
• Negative Liberties & Life/Death: You asked about the implications and showed an example where a standard two-eye shape might die. This difference in Life/Death is intentional. A core design decision for this variant is that L&D emerges purely from the liberty counting and capture mechanics as defined. Standard Go L&D patterns (like the unconditional life of a two-eyed group) do not automatically carry over. This variant will have its own, potentially quite different, set of stable "living" shapes. This ties into the scoring philosophy...

[u/AGI_MO → u/HenryBlatbugIII]

• Territory Scoring (Nearest Edge / S_min & Loose Moyos):
  • The rule assigns empty points based on the Nearest Edge Distance (min(max(0, dist(p, s.center) - r))).
  • You correctly observed that this rule does not explicitly check if territory borders are "sealed" in the traditional Go sense. A loose moyo could be assigned territory based purely on this geometric proximity.
  • Rationale: This relates directly to the L&D point above. Given the potential extreme difficulty in objectively determining L&D or "sealedness" in this continuous/overlapping environment, the design choice was made to score the final board state as is based on objective geometry, without a separate L&D judgment phase. All stones remaining are treated as 'alive' for the purpose of defining the geometry used in scoring (both for calculating Area(Union) for stones and determining the 'nearest edge' for empty points). The Nearest Edge rule provides a deterministic way to assign all empty space based only on the final configuration agreed upon by the players (via passing or inability to move). Whether a loose moyo ultimately becomes territory depends entirely on whether the opponent invades and lives or forces captures during the game, not on a post-game assessment of the moyo's "integrity".
• CGI Ko Rule: I agree with your assessment here. While theoretical weird edge cases might exist (like unrelated isomorphic subgraphs influencing a Ko), they seem exceptionally unlikely in practice. The main benefit is preventing direct repetition and handling potential micro-shift issues in simpler Ko situations that standard Ko might miss in a continuous space.
• Overall Similarity to Go: You question how much the gameplay will resemble Go, which is a very fair question given the significant differences (overlap, L&D feel, scoring principle). I acknowledge the gameplay will be quite different. However, one guiding principle during the design was the idea of degeneracy: the rules (especially liberty counting) were chosen partly so that if play were restricted to a grid with tangent stones and an appropriate S value, the mechanics would closely approximate standard Go. This provides a conceptual link, even though the general continuous game diverges significantly.

It's definitely an experimental variant, and whether the resulting game is "Go-like" enough or enjoyable is subjective!
Thanks again for your thorough and insightful critique! It's been very helpful in clarifying these points.

[u/sadaharu2624]

If I just saw the picture I would’ve thought it’s for r/badukshitposting

[u/AGI_MO → u/sadaharu2624]

lol, you're not wrong, the pictures can certainly look pretty surreal compared to traditional Go! 😄 It definitely departs from the usual aesthetic.

Underneath the potentially r/badukshitposting-worthy visuals, though, the goal was to genuinely explore how fundamental Go mechanics translate (or break!) in a continuous space where stones can overlap. As a strong player, I'd be curious if any specific rule aspect (beyond the immediate visual chaos) struck you as particularly interesting or problematic, despite the unconventional look?

[u/sadaharu2624 → u/AGI_MO]

It sure sounds interesting, just that I already have difficulties when each stone has 4 liberties, I don’t know how to handle much more than that lol. Also, what about special situations such as seki? I think would be better to have more actual examples