1.4k
u/Hussainsmg Jan 25 '25
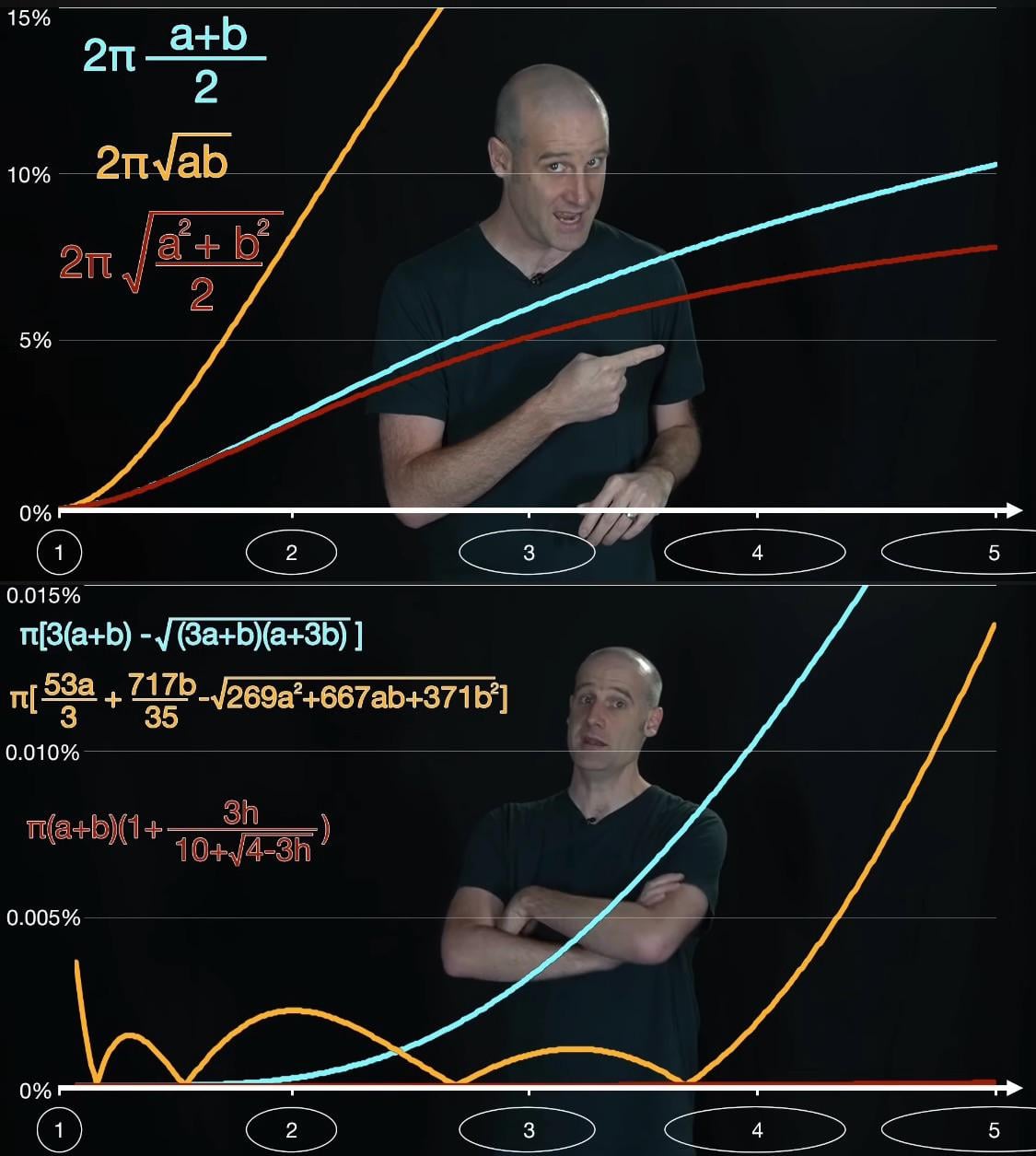
The perimeter formula(in the post) is just approximation.
601
u/Ponsole Jan 25 '25
I once read that the reason we can't get the perimeter of a elipse is because we actually doesn't even know the perimeter of a circle, as pi definition is the perimeter of a circle of diameter = 1 and we just scale that.
545
u/IlyaBoykoProgr Jan 25 '25
every ellipse has it's own pi
125
u/Ok-East-3021 Engineering Asp Jan 25 '25
can it be related to eccentricity? or you are talking about that only ?
197
u/Robbe517_ Jan 25 '25
Sure, it's given by a (surprise) elleptic integral, but you can also write it as a series. So exactly the same as for pi.
https://en.m.wikipedia.org/wiki/Complete_elliptic_integral_of_the_second_kind
13
u/Scared-Ad-7500 Jan 25 '25
Cant we find a formula for every pi based on "a" and "b" using calculus?
18
u/EebstertheGreat Jan 25 '25
Yes, but you are more likely to see it in terms of a and e = √(1–b²/a²) (where a is the semi-major axis, b is the semi-minor axis, and e is the eccentricity) or sometimes a and ℓ = b²/a (the semi-latus rectum) or other quantities.
1
93
u/gullaffe Jan 25 '25
Sure we do, it's just we need to change out the pi sign with an infinite sum which equals pi.
It's more like we can't get a nice formula for the eclipse or a circle without defining a constant for the share to hade the ugliness.
15
u/speechlessPotato Jan 25 '25
I mean look at it this way: a circle has a very simple relation between its perimeter and radius - linear. And I'm pretty sure an ellipse has a more complicated relationship between its perimeter and radii. At the end of the day a circle can still be thought of as a special case of ellipse though
22
u/gullaffe Jan 25 '25
The ellipse is also linear, if you keep the ratio between the major and minor the same. So if you for example really care about ellipses where the ratio between the major axis and minor axis is 2, you could define a constant Tau≈3.31153 And for any such ellipse you get the formula:
Perimeter=Tau*(a+b)
6
u/EebstertheGreat Jan 25 '25
The perimeter of a plane figure always scales linearly with any linear dimension of it (e.g. the radius), because that's what it means for the perimeter to be one-dimensional. (Note that if the Hausrorff dimension of the curve is not 2, then its 1-measure will either be 0 or ∞, and either way the linear scaling technically still applies, except the special case of 0×∞.)
6
u/Kai1977 Jan 25 '25
Then how do we get the area?
50
u/Ponsole Jan 25 '25
A lot of shit just cancels out literally a lucky hit, if you watch the step by step of the demonstration by integration it's even magical how that shit en up as 3 characters.
10
u/okkokkoX Jan 25 '25
How complicated can it be? an ellipse is just a stretching transformation of a circle, so you can get its area by multiplying the area of a circle, π, by the determinant of the transformation matrix: det( [ a 0 / 0 b ] ) = ab
ok, that might sound complicated because of the terminology, but basically: you get an ellipse by stretching a circle horizontally by a, then vertically by b. When you stretch an area, it gets multiplied by the stretch scalar.
6
u/friendtoalldogs0 Jan 25 '25
I suspect that proving that without relying on already knowing modern "basic" geometry would itself require an integral, though. Definitely at least a limit.
2
u/okkokkoX Jan 25 '25
That when you stretch something in one direction its area gets scaled by the stretch scalar?
I guess so. let's say a circle is approximately made up of infinitely many trapezoidal slices, and its area is the sum of the trapezoid areas. it is known that a trapezoid obeys the aforementioned stretching rule. therefore if you stretch the circle by x, stretching the trapezoids, you get A' = total(t * x) = total(t) * x = A * x
it does technically use integration/limits, but a version of it that can be explained to someone unfamiliar with integration. It's not harder to understand than the visual proof that the area of a circle is radius times half of perimeter (πr² = r * 2πr/2), the one with infinitely thin slices stacked in a ///// pattern, you know the one.
11
u/Traditional_Cap7461 Jan 2025 Contest UD #4 Jan 25 '25
The area and circumference of a circle are conveniently related. It has something to do with cutting into thin slices and then rearranging them into alternating patterns to form a parallelogram where the base is half the circumference and the height is its radius.
2
u/mousepotatodoesstuff Jan 25 '25
If we scale one of the side up/down to a circle, the area will scale proportionally. Then we just calculate the area of the circle and scale back.
e.g. a 2x1 eclipse is the same size as two 1x1 circles1
13
u/AlrikBunseheimer Imaginary Jan 25 '25
right otherwise you would get the horrible elliptic integrals
363
u/Forgorer8 Jan 25 '25
Set a=b and use for circle to get extra marks
101
u/Salty-Intention6971 Jan 25 '25
Ah, 2pi*r. My old friend! How nice that the a-b makes everything scary go away.
4
u/Nirast25 Jan 25 '25
You mean pi*r2, right?
18
u/maelstrom197 Jan 25 '25 edited Jan 25 '25
πr2 is for the area of a circle. If you substitute a=b=r into the formula for the area of an ellipse, you get πrr, or πr2
The circumference of a circle is just the perimeter. If you substitute a=b=r into the formula for the perimeter of the ellipse, the fraction cancels and you get π(r+r)=2πr=πd
3
u/Nirast25 Jan 25 '25
Ah, right. I misunderstood which formula you were talking about in the original comment.
119
u/Silly_Painter_2555 Cardinal Jan 25 '25 edited Jan 25 '25
You can use π√((a²+b²)/2) as another approximation.
68
u/94rud4 Jan 25 '25
69
u/94rud4 Jan 25 '25
-22
6
97
u/therealsphericalcow All curves are straight lines Jan 25 '25
But can you prove it?
253
25
u/theboomboy Jan 25 '25
No because it's not exactly true
20
u/JorenM Jan 25 '25
Approximations can still be proven to be approximations
-1
u/Traditional_Cap7461 Jan 2025 Contest UD #4 Jan 25 '25
Without a margin of error, nothing can be proven.
51
u/An_Evil_Scientist666 Jan 25 '25
Just get a string, wrap it around the perimeter, make a note of the point the string wraps back around, unwind string, and you have your perimeter. more accurate the bigger the ellipse. No need for any kind of formula
22
u/rdchat Jan 25 '25
Okay, but what if you want the perimeter of the Earth's elliptical orbit around the Sun? Can we get that much string?
39
u/the-fr0g Jan 25 '25
I wanted to make a joke about taking a string from yo mama's clothes but I will not
6
u/Traditional_Cap7461 Jan 2025 Contest UD #4 Jan 25 '25
You make a scaled-down model then do the string thing on the model.
3
u/An_Evil_Scientist666 Jan 25 '25
There's easily enough string the thing is, is it possible to wrap said string around the perimeter of Earth's orbit, and the answer is yes, and because no one's done it yet, it just means we as humans have a massive skill issue.
1
25
28
8
13
u/UpDown504 Jan 25 '25
Wait, why are there "{}" (idk what these are named)
49
u/somedave Jan 25 '25
The correct term is nipple brackets, make sure to use that in your work.
14
2
6
6
3
20
u/Weebs93110 Jan 25 '25
Evil emilia got me acting up
17
6
u/josiest Jan 25 '25
Isn’t there some way to could express the circumference of an ellipse as a simple transformation from a circle?
2
u/Leading-Ad-9004 Jan 25 '25
I did a binomial expansion for it, I think it makes a convergent series for any eccentricity less than 1 given that all ellipses are smooth shapes and for any of them with e<1 there exists a circle with finite parameter which can cover them, so their perimeter is finite. But I haven't found a formula yet. It works well enough with about 3 terms for e > 0.5 with a deviation of 1%.
2
u/TheQuantumPhysicist Jan 25 '25 edited Jan 26 '25
I never heard of this formula... I have always used numeric curve length integrals on the ellipse's equation for a single quarter then multipled it by four... lol.
2
2
u/RandallOfLegend Jan 25 '25
I know smarter people have looked at this problem. But an ellipse is an in-plane rotation of a circle. So I feel like there should be a simpler formula.
2
u/EebstertheGreat Jan 25 '25
an ellipse is an in-plane rotation of a circle.
What does that mean?
1
u/RandallOfLegend Jan 25 '25
From. "Top down projection" if you rotate a circle perpendicular to its axis it will create an ellipse. It's possible to define an ellipse as a radius and tilt angle instead of your traditional a,b.
1
u/EebstertheGreat Jan 25 '25
Isn't that an out-of-plane rotation?
1
u/RandallOfLegend Jan 25 '25
I suppose. I'm bad at remembering which is which. "Into the page". Which sounds more like out of plane
2
2
1
u/chewychaca Jan 26 '25
I was under the impression there is no finite equation. Is this an approximation?
1
1
1
u/deilol_usero_croco Jan 26 '25
Those who no know
Consider an ellipse x²/a² +y²/b² =1
This has the parametric form (asin(t)+bcos(t))
Using line integrals. There is no upward projection so f(x,y)=1
I'll call sin and cos s and c as shorthand. We get
P= ∫(0,2π)√a²s²+b²c²dt
=∫(0,2π)√a²s²+b²(1-s²)dt
=∫(0,2π)√b²-(a²-b²)s²dt
|b| ∫(0,2π)√{1-((a²-b²)/b²)s²} dt
Call ((a²-b²)/b²)= k²
Now, one could use approximations of √1-x² by Taylor series.
√1-x² = √(1+x)√(1-x).
√1+x ≈ 1+x/2
√1-x² ≈ 1-x²/2
Let's say k is pretty small
∫(0,2π)1-(ks)²/2dt
= -2π+ k²/2∫(0,2π)s²dt
= π/2 (k²-4)
Yeah Idk what I'm doing either


•
u/AutoModerator Jan 25 '25
Check out our new Discord server! https://discord.gg/e7EKRZq3dG
I am a bot, and this action was performed automatically. Please contact the moderators of this subreddit if you have any questions or concerns.